In this article I’m trying to modelozie the basic Sets theory operation by programming , Sets theory is a fundamental concept helping Developers and Software architects to implement some good generic algorithms in order to solve problems in a generic vision, generally this kind of solution is useful and appreciated by Design Pattern architects.
To modelize things we selects very basic operations to implement , because basics are fundamental for extending model into a complex model , the abstraction is playing a big role in Design Pattern , that’s why I implement a generic class so later by extending It can be applied to lots of scenario.
In mathematics a Set is a collection of elements or objects with no necessary links between elements,
A = {1,7,8,25,17,9,30,42,70,18,25,99,55,88}
B = {2,27,8,88,18}
C = {“one”,”two”,”three”,”four"}
D = {🇨🇦,🇨🇿,🇨🇭,🇫🇷,🇺🇸}
//union of C and D
A ∪ B = {1,2,7,8,25,27,17,18,9,30,42,70,18,25,99,55,88}
//Intersection of A and B
A ∩ B = {8,88,18} //union of A and B
//union of C and D = C + D
C ∪ D = {“one”,”two”,”three”,”four”,🇨🇦,🇨🇿,🇨🇭,🇫🇷,🇺🇸}
//Intersection of A and B
A ∩ C = ∅
//substraction of A and B
A - B = {1,7,25,17,9,30,42,70,25,99,55}
Now we are going to implement programmatically those basic ∪ (union) , ∩ (intersection), - (Subtract)
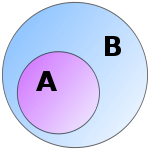
Subset
A is a subset of B when all members of A are also member of B ∀ x ∈ A => x ∈ B
A = {1,2,4,6,b} , B= {4,b,a,d,f,c}
A ∪ B = {1,2,4,6,b,a,d,f,c} => ∀ x ∈ A ∨ x ∈ B
A ∩ B = {4,b} => ∀ x ∈ A ∧ x ∈ B
A - B ={1,2,6} => ∀ x ∈ A ∧ x ∉ B
We create a generic class let’s call MathArray , to simplify things and in order to be able to check equality of elements (avoid to overload an additional equality operator) let’s suppose a generic type of Equatable class.
we add a list of items and a convenience initializer for default purpose
public class MathArray<T:Equatable>{
var mItems = [T]()
var items: [T]{
get {
return self.mItems
}
set{
self.mItems = newValue
}
}
public convenience init(){
let arr = Array<T>()
self.init(array: arr)
}
public init(array:[T]){
items = array
}
}
One of the great power of Swift is Overloading , those C++ developers are probably familiar with the nice C++ ability to define or redefine operators like +,-,==,&
for example it will be nice to define + operator to operate on any object we like , I mean by defining it we can apply it to A and B to get union A ∪ B as A+B , or we can define A - B or …
let union = A + B [or = A ∪ B]
let subtract = A - B
we can also check a collection if it’s a subset of another collection as
let isSubset = A ⊂ B
Now we implement all those nice operators in a global scoop
//give operator , this operator is exclusively used for debugging and test purpose
prefix func => <T>(right:MathArray<T>)->[T]{
return right.items
}
//Minus operator
func - <T>(left:MathArray<T>,right:MathArray<T>)->[T]{
let check = {
(x:T)->Bool in
return right.items.indexOf(x)==nil
}
return left.items.filter(check)
}
//subset operator
func ⊂ <T>(left:MathArray<T>,right:MathArray<T>)->Bool{
for element in left.items {
guard right.items.indexOf(element) != nil else { return false}
}
return true
}
//equal operator
func == <T>(left:MathArray<T>,right:MathArray<T>)->Bool{
for element in left.items {
guard right.items.indexOf(element) != nil else { return false}
}
for element in right.items {
guard left.items.indexOf(element) != nil else {return false}
}
return true
}
// union operator, + operator can be also replaced by ∪
func + <T>(left : MathArray<T>,right : MathArray<T>)->[T]{
var result = [T]()
for element in left.items{
result.append(element)
}
for element in right.items{
result.append(element)
}
return result
}
//intersection operator
func ∩ <T>(left : MathArray<T>,right : MathArray<T>)->[T]{
let check = {(x:T)->Bool in return right.items.indexOf(x) != nil}
return left.items.filter(check)
}
//Full class implementation , compiled & tested with Swift2 on XCODE 7.2
import Foundation
import UIKit
public class MathArray<T:Equatable>{
var mItems = [T]()
var items: [T]{
get {
return self.mItems
}
set{
self.mItems = newValue
}
}
public convenience init(){
let arr = Array<T>()
self.init(array: arr)
}
public init(array:[T]){
items = array
}
public static func getUnion<T:Equatable>(array1:[T],array2:[T])->[T]{
return MathArray<T>(array: array1)+MathArray<T>(array: array2)//add
}
public static func getInterset<T:Equatable>(array1:[T],array2:[T])->[T]{
return MathArray<T>(array: array1) ∩ MathArray<T>(array: array2)
}
public static func isSetsEqual<T:Equatable>(array1:[T],array2:[T])->Bool{
return MathArray<T>(array: array1) == MathArray<T>(array: array2)
}
public static func isSubset<T:Equatable>(array1:[T],array2:[T])->Bool{
return MathArray<T>(array: array1) ⊂ MathArray<T>(array: array2)
}
public static func subtract<T:Equatable>(array1:[T],array2:[T])->[T]{
return MathArray<T>(array: array1) - MathArray<T>(array: array2)//minus
}
public static func getItemsForArray<T:Equatable>(array:[T])->[T]{
return =>MathArray<T>(array: array)
}
}
//Here we overload our Sets operators , notice overloading is only allowed in a global scoop
//so we define our Overloaded Operator out of our class
infix operator ∩ {}
prefix operator => {}
infix operator ⊂ {}
prefix func => <T>(right:MathArray<T>)->[T]{
return right.items
}
//Minus operator
func - <T>(left:MathArray<T>,right:MathArray<T>)->[T]{
let check = {
(x:T)->Bool in
return right.items.indexOf(x)==nil
}
return left.items.filter(check)
}
//subset operator
func ⊂ <T>(left:MathArray<T>,right:MathArray<T>)->Bool{
for element in left.items {
guard right.items.indexOf(element) != nil else { return false}
}
return true
}
//equal operator
func == <T>(left:MathArray<T>,right:MathArray<T>)->Bool{
for element in left.items {
guard right.items.indexOf(element) != nil else { return false}
}
for element in right.items {
guard left.items.indexOf(element) != nil else {return false}
}
return true
}
// union operator
func + <T>(left : MathArray<T>,right : MathArray<T>)->[T]{
var result = [T]()
for element in left.items{
result.append(element)
}
for element in right.items{
result.append(element)
}
return result
}
//intersection operator
func ∩ <T>(left : MathArray<T>,right : MathArray<T>)->[T]{
let check = {(x:T)->Bool in return right.items.indexOf(x) != nil}
return left.items.filter(check)
}
===========================================================
To test the class we can for example :
let A = [5,17,9,30,42,70,18,25,99,55,88]
let B = [5,25,61,54]
let result = MathArray<Int>.subtract(A, array2: B)
print("\(result)”)
print => [61,54]